When waves are incident on a sample with regular lattice layers, an interference pattern can be observed. The angular positions where constructive interference is visible can be related to the wavelength ‘λ’ and the lattice spacing ‘d’ lambda and the lattice spacing noted as 'd' by Bragg’s Law:
2d sin(θ)=nλ,two d times sinus of angle theta equals n times lambda
where ‘θ’ is the incident and reflected angle of a scattered wave and ‘n’ is a positive integer usually set equal to one.where theta is the incident and reflected angle of a scattered wave and n is a positive integer usually set equal to one.
This equation can be derived geometrically by looking at the figure. Consider two coherent waves reflecting from two planes of atoms. The path difference between the waves (shown in purple) can be found using trigonometry to be 2d sin(θ). If this path difference is equal to an integer number of wavelengths (nλ) two d times sinus of angle theta. If this path difference is equal to an integer number of wavelengths, n times lambda, the scattered waves will still have zero phase difference after reflection. If this condition is met, the peaks and troughs of the waves will align, constructively interfering to create a bright fringe in the interference pattern. Because the waves remain coherent during this process, this is known as coherent scattering.
By controlling the wavelength of light and recording the scattering angle (2θ), Bragg’s law can be rearranged to measure the lattice spacing d. This can be used to help determine the lattice structure of known samples or identifying unknown samples.
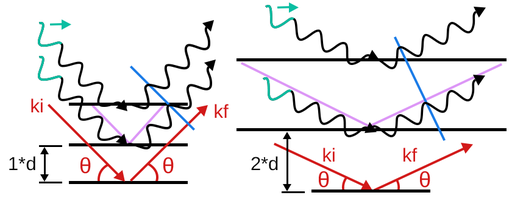
Figure. A schematic view of Bragg's law.