Ellipses

An ellipse is a stretched circumference. Every point in a circumference is at the same distance from its center. When we stretch a circumference to create an ellipse, its center splits into two different points we call foci (each of the foci is called a focus). The sum of the distances to each focus is always the same for every point in the ellipse.

The widest axis of the ellipse is called its major axis. You can think of it as the axis that has been stretched to create an ellipse from a circle. Each half of the major axis is a semimajor axis. Both foci sit on the major axis, at symmetrical points from the center of the ellipse.

The shorter axis of an ellipse is called the minor axis. You can think of it as the part of the ellipse that has been shortened by the stretching. The major axis and the minor axis are perpendicular and they intersect at the center of the ellipse.

The eccentricity of an ellipse is a measure of how much it deviates from a circumference, and it is a number between zero and one. It is the quantity of “stretching” that we need to create that ellipse from a circumference. An ellipse of eccentricity zero is a circumference, and the flatter an ellipse becomes, the more its eccentricity approaches one.

The eccentricity, e, can be calculated using the formula: e = f/d, where f is the distance between the foci of the ellipse, and d is the ellipse’s major axis length.

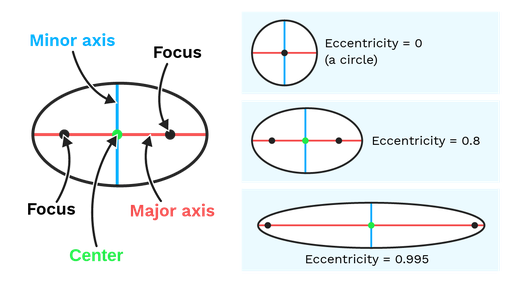
Figure: On the left, parts of an ellipse. To the right, ellipses of different eccentricities.